Some remarks about computation times
It is commonly known amongst number theorists that
-
modular exponentiation (the (important) computation of
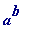 mod
n
) can be performed quickly, while
mod
n
) can be performed quickly, while
-
factorial modular computation (
a
! mod
n
) is (currently) relatively slow; Richard Crandall (
Topics in Advanced Scientific Computation
, Springer-Verlag (1996)) remarks:
"
Before we investigate ways to compute
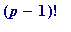 it is worth noting that factorial evaluation must in general be problematic. One way to see this is, if we wanted to factor some number N, and if it were easy to find massive
factorials
M
!
mod
N
where
M
is say of order
it is worth noting that factorial evaluation must in general be problematic. One way to see this is, if we wanted to factor some number N, and if it were easy to find massive
factorials
M
!
mod
N
where
M
is say of order
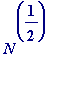 or even some lower but significant power of
N
,
the one could simply take the GCD of the factorial with
N
routinely to produce factors of
N
. On the belief that factorisation is intrinsically difficult, it must follow that so, too is factorial evaluation. Another way to say this is, a factorial M! contains some information about every integer not exceeding M
."
or even some lower but significant power of
N
,
the one could simply take the GCD of the factorial with
N
routinely to produce factors of
N
. On the belief that factorisation is intrinsically difficult, it must follow that so, too is factorial evaluation. Another way to say this is, a factorial M! contains some information about every integer not exceeding M
."
A hasty demonstration
. The following computes the remainder that
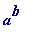 leaves on division by
n
, for the assigned values of
a
,
b
and
n. A
word of
warning
, though, for the uninitiated: it is done -
not by first
calculating the actual value of
leaves on division by
n
, for the assigned values of
a
,
b
and
n. A
word of
warning
, though, for the uninitiated: it is done -
not by first
calculating the actual value of
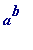 and then dividing by
n
(that would have been attempted had one (foolishly) used the command
a^b mod n
) -
but rather by
using congruence technique together with the
square and multiply
method (that method is invoked with the use of '&' in the command
a&^b mod n
).
and then dividing by
n
(that would have been attempted had one (foolishly) used the command
a^b mod n
) -
but rather by
using congruence technique together with the
square and multiply
method (that method is invoked with the use of '&' in the command
a&^b mod n
).
>
a :=
599999999999999999999999999777777777777777777777777777777777777777777777777777777777777:
b := 38888888888888866666666666664444444444444444444444333333333333300000000000999999999999:
n := 766666666666666666666888888888888888888888555555555555555555555555555555555555557777777778888888888888888855555555555555544444444444444444444444444444444444321:
a&^b mod n;
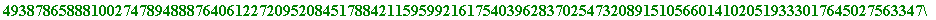
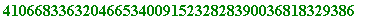
>
Suppose, now, that one wanted to compute the
remainder that
M
! leaves on division by
N
(the type of computation of which Richard Crandall speaks above, and which - as you will see - is at the heart of this talk...) for given
M
and
N
.
(Incidentally, although modular exponentiation may be performed extremely quickly, if one makes the modulus 'n' be very large then the time taken becomes the greater... In 2002, just before I was to give a talk in Dallas on my 'Fermat 6' work, I wrote to Richard Crandall to ask his estimate for how long it would take to test the possible primality of the 31st Fermat number
![F[31] = 2^(2^31)+1](images/reduced TCD talk 9th Feb 2005704.gif) , which is
entirely decided
(using P�pin's theorem) by the modular exponentiation computation of
, which is
entirely decided
(using P�pin's theorem) by the modular exponentiation computation of
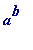 mod
n
, with
mod
n
, with
![a = 3, b = (F[31]-1)/2, n = F[31]](images/reduced TCD talk 9th Feb 2005706.gif)
By P�pin's theorem, if
![3^((F[31]-1)/2) = -1](images/reduced TCD talk 9th Feb 2005707.gif) (mod
(mod
![F[31]](images/reduced TCD talk 9th Feb 2005708.gif) ) then
) then
![F[31]](images/reduced TCD talk 9th Feb 2005709.gif) is prime.
is prime.
(Note in passing. At that time
![F[31]](images/reduced TCD talk 9th Feb 2005710.gif) was the
smallest
Fermat number whose status was unknown:
was the
smallest
Fermat number whose status was unknown:
![F[0], `...`, F[4]](images/reduced TCD talk 9th Feb 2005711.gif) all being prime, while every one of
all being prime, while every one of
![F[5], `...`, F[30]](images/reduced TCD talk 9th Feb 2005712.gif) was known to be composite. Later that year a factor of
was known to be composite. Later that year a factor of
![F[31]](images/reduced TCD talk 9th Feb 2005713.gif) was found by Kruppa and Forbes - it was the 23-digit prime (5463561471303*
was found by Kruppa and Forbes - it was the 23-digit prime (5463561471303*
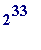 +1) - and now
+1) - and now
![F[33]](images/reduced TCD talk 9th Feb 2005715.gif) is the smallest Fermat number of unknown status. Anyone interested in reading more about Fermat numbers might like to access the Fermat Record Number corner of my website.)
is the smallest Fermat number of unknown status. Anyone interested in reading more about Fermat numbers might like to access the Fermat Record Number corner of my website.)
Richard (who perhaps knows more than anyone about such matters) responded that it would take more than
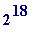 years...
)
years...
)
____________________
Here is a simple procedure for performing factorial modular reductions:
>
fact_rem := proc(M, N) local r, k;
r := 1; for k from 2 to M do
r := k*r mod N od; r; end:
This computes the remainder 8! leaves on division by 17:
>
fact_rem(8, 17);
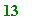
This computes the remainder 20! leaves on division by (Jacobi prime) 61:
>
fact_rem(20, 61);
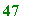
This computes the remainder 6000! leaves on division by (prime) 8191:
>
fact_rem(6000, 8191);
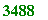
>
Time (tongue-in-cheek) note
#1. It took as long as 80.5 hours on a 2.8GHz Pentium 4 merely to verify (using straightforward modular reduction) that
p
= 18711862657 satisfies the congruence
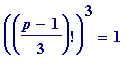 (mod
p
), while the identification of that prime, as a possible candidate for satisfying
(mod
p
), while the identification of that prime, as a possible candidate for satisfying
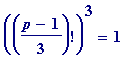 (mod
p
), took only a matter of minutes using the alpha-criterion. Another verification, using an intermediary stage criterion that presented itself to me - what I later call the cubes-odd-square criterion - took only a microsecond.
(mod
p
), took only a matter of minutes using the alpha-criterion. Another verification, using an intermediary stage criterion that presented itself to me - what I later call the cubes-odd-square criterion - took only a microsecond.
Roughly how long would it have taken to verify that
p
=
16426761041360671
satisfies
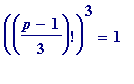 (mod
p
), using modular reduction?
Over 8000 years:
(mod
p
), using modular reduction?
Over 8000 years:
>
floor(16426761041360671/18711862657);
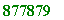
>
hours := (16426761041360671/18711862657)*(80.5);

>
years := floor(hours/(24*365));
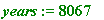
>
Time (tongue-in-cheek) note
#2.
Roughly how long does/would it take (on a Pentium of known speed) to verify (using step-by-step modular reduction) that a given prime
p
= 1 (mod 3) satisfies the congruence
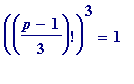 (mod
p
) ... (1)
(mod
p
) ... (1)
Time (comparison) note
. It took as long as 80.5 hours (using a 2.8GHz Pentium) to verify that
p
= 18711862657 satisfies (1), while the
identification
of that prime, as a
possible
candidate for satisfying (1) took only a matter of minutes using the alpha-criterion. A verification, using the cubes-odd-square criterion, took only a microsecond.
Time (crude under) estimates
. Suppose
p
and
q
are primes (both 1 mod 3), and that
q
~
mp
(think of
m
as a multiplier, which in usage will be on the large side). Suppose also that the computation of
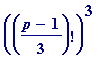 mod
p
takes time
t
; then the computation of
mod
p
takes time
t
; then the computation of
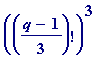 mod
q
will take time
mt
, at least.
mod
q
will take time
mt
, at least.
Simple demonstration (on a 1.7GHz)
. I will demonstrate using two primes
p
= 1000003 and
q
= 2000029, the first after 1 and 2 million respectively:
>
for p from 10^6 by 3 do
if isprime(p) then print(p); break; fi; od;
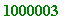
>
for q from (2*10^6+2) by 3 do
if isprime(q) then print(q); break; fi; od;
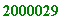
>
P[1,3] := proc(p) local r, k; r := 1;
for k from 2 to (p-1)/3 do
r := mods(r*k, p) od; r; end:
>
p := 1000003: P[1,3](p); # took 2.2 secs
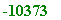
>
q := 2000029: P[1,3](q); # took 4.4 secs
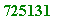
One further simple demonstration (on a 1.7GHz)
. I will demonstrate using two primes
p
= 10000141 and
q
= 20000023, the first after 10 and 20 million respectively:
>
for p from 10^7 by 3 do
if isprime(p) then print(p); break; fi; od;
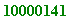
>
for q from (2*10^7+2) by 3 do
if isprime(q) then print(q); break; fi; od;

>
p := 10000141: P[1,3](p); # took 23.9 secs
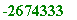
>
q := 20000023: P[1,3](q); # took 49.1 secs
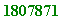
>
8000+ years
. I came upon prime
p
= 16426761041360671 (a prime value of
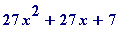 ), while searching for primes
p
such that (
), while searching for primes
p
such that (
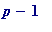 ) has a large number (10, 11, 12, ... ) of
distinct
prime factors (apart from the singleton 3).
) has a large number (10, 11, 12, ... ) of
distinct
prime factors (apart from the singleton 3).
(Its details:
24665736, 16426761041360671, (2)(3)(5)(7)(11)(13)(17)(19)(23)(41)(59)(61)(499), [12]
It was actually the
first instance
of a '[12]' (i.e., 13 primes - including the '3' - in the prime factorisation of
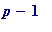 )).
)).
How long it would take - for comparison with the 2.8GHz, crudely underestimated - to verify (1) for that
p
, using modular reduction; it comes out at ~ 8067 years:
>
>
p1 := 18711862657; # the 80.5 hours base example
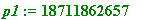
>
p2 := 16426761041360671;
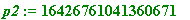
>
m2_1 := floor(p2/p1); # how much longer
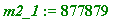
>
hours2 := (m2_1)*(80.5);
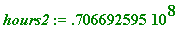
>
years2 := floor(hours2/(24*365));
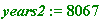
>
Thus p2 = 16426761041360671 would take a minimum of 8067 years.
Finally, just for fun, I wanted to find a prime p3 that would take at least the (commonly quoted) age of the universe to
verify
(1), that prime being found using
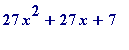 (itself a proof), or further verification using the cube-odd square test.
(itself a proof), or further verification using the cube-odd square test.
>
m3_2 := floor(15000000000/years2);
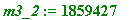
I want a prime p3 (= 27*x^2 + 27*x + 7) which is at least 'MIN', defined by:
>
MIN := p2*m3_2;
f := x -> 27*x^2 + 27*x + 7;
fsolve(f(x) = MIN);

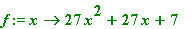
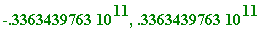
To have
candidate
x's making (prime)
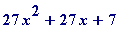 be large enough,
x
needs to have
minimum
value:
be large enough,
x
needs to have
minimum
value:
>
x := 33634397628: is(f(x-1) > MIN); is(f(x) > MIN);

>
for x from 33634397628 do
if isprime(f(x))
then print(f(x));
break; fi od;
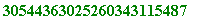
>
p3 := f(x);
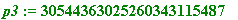
>
M3_2 := floor(p3/p2); # is, unsurprisingly, m3_2
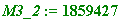
>
sqrt(((p3 - 1)/3)^3 mod p3); # is an odd number (takes a microsecond)
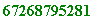
>
Summary
. To test (1) for the prime p3 = 30544363025260343115487 would take at least 15,000,000,000 years.
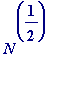 or even some lower but significant power of
N
,
the one could simply take the GCD of the factorial with
N
routinely to produce factors of
N
. On the belief that factorisation is intrinsically difficult, it must follow that so, too is factorial evaluation. Another way to say this is, a factorial M! contains some information about every integer not exceeding M
."
or even some lower but significant power of
N
,
the one could simply take the GCD of the factorial with
N
routinely to produce factors of
N
. On the belief that factorisation is intrinsically difficult, it must follow that so, too is factorial evaluation. Another way to say this is, a factorial M! contains some information about every integer not exceeding M
."![F[31] = 2^(2^31)+1](images/reduced TCD talk 9th Feb 2005704.gif) , which is
entirely decided
(using P�pin's theorem) by the modular exponentiation computation of
, which is
entirely decided
(using P�pin's theorem) by the modular exponentiation computation of
![a = 3, b = (F[31]-1)/2, n = F[31]](images/reduced TCD talk 9th Feb 2005706.gif)
![3^((F[31]-1)/2) = -1](images/reduced TCD talk 9th Feb 2005707.gif) (mod
(mod
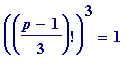 (mod
p
), while the identification of that prime, as a possible candidate for satisfying
(mod
p
), while the identification of that prime, as a possible candidate for satisfying
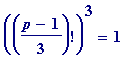 (mod
p
), took only a matter of minutes using the alpha-criterion. Another verification, using an intermediary stage criterion that presented itself to me - what I later call the cubes-odd-square criterion - took only a microsecond.
(mod
p
), took only a matter of minutes using the alpha-criterion. Another verification, using an intermediary stage criterion that presented itself to me - what I later call the cubes-odd-square criterion - took only a microsecond.
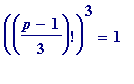 (mod
p
), using modular reduction?
Over 8000 years:
(mod
p
), using modular reduction?
Over 8000 years:
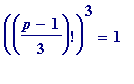 (mod
p
) ... (1)
(mod
p
) ... (1)
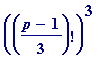 mod
p
takes time
t
; then the computation of
mod
p
takes time
t
; then the computation of
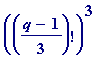 mod
q
will take time
mt
, at least.
mod
q
will take time
mt
, at least.
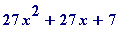 ), while searching for primes
p
such that (
), while searching for primes
p
such that (
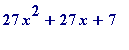 (itself a proof), or further verification using the cube-odd square test.
(itself a proof), or further verification using the cube-odd square test.
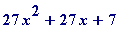 be large enough,
x
needs to have
minimum
value:
be large enough,
x
needs to have
minimum
value: